from __future__ import unicode_literals #ékezetes betűk
Integrálás python-al¶
01-Egyszerű numerikus integrálás¶
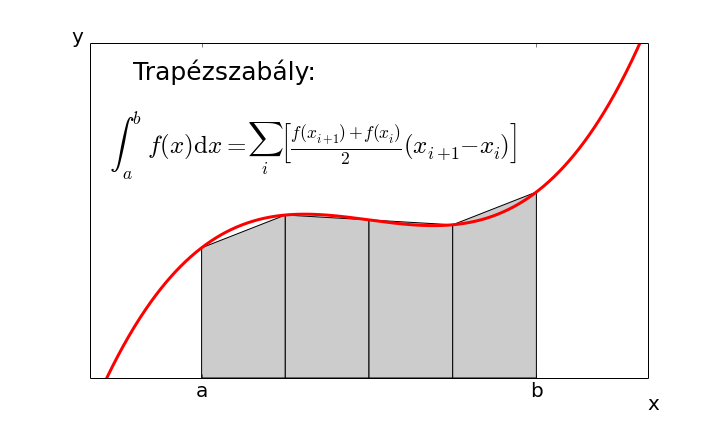Sok gyakorlati alkalmazásban előkerül egy fügvény integráljának, azaz a függvény görbéje alatti területnek a meghatározása. Sok analitikus függvény integrálját zárt alakban meg lehet határozni. A gyakorlatban viszont sokszor nem ismert a függvény analitikus alakja. Gondoljunk itt például egy zajos mérésre. Ilyen esetben a függvény integrálját a rendelkezésre áló mérési pontok \(x_0,x_1,x_2,\dots x_j,\dots\) és mért értékek \(f_0,f_1,f_2,\dots f_j,\dots\) alapján kell valahogy meghatároznunk. Ekkor az integrál értékét rendszerint egy véges összegzéssel határozhatjuk meg ahol az összeadandó értékek a mérési pontok és a mért mennyiségek valamilyen függvényei. Az egyik legegszerűbb, és meglepően jól használható közelítés az úgynevezett trapéz szabály:\[\int_a^b \mathrm{d}xf(x)\approx\sum_i \frac{(f_{i+1}+f_i)}{2}(x_{i+1}-x_i)\] Írjunk egy egyszerű függvényt amely a trapéz szabály alkalmazásával két számsorozatból (\(x_i\) és \(f_i\)) meghatározza egy függvény integrálját!
def trapez(x,y):
#x a mintavételezési pontokat tartalmazó számsorozat
#y pedig a függvényértékeket tartalmazó számsorozat mégpedig y_i=f(x_i) alakban
#x és y mindenképp legyenek ugyanolyan hosszúságú tömbök !
#x pedig szigorúan növekvősorrendben tartalmazza a mintavételezési pontokat!
osszeg=0.0
for i in range(len(x)-1): #mivel az utolsó pontnál i+1 már nincs ezért elég csak az utolsó előtti értékig elmenni!
osszeg=osszeg+0.5*(y[i+1]+y[i])*(x[i+1]-x[i])
return osszeg
Egyszerű polinomiális függvény integrálása és a relatív hiba¶
Vizsgáljuk meg az \(f(x)=x^2+3x+2\) függvény \([0,1]\) intervallumon vett integrálját a fent definiált trapéz formulát implementáló rutin segítségével! Vizsgáljuk meg hogy az integrál értéke hogy változik a mintavételezési pontok számának növelésével! Hány mintavételezési pontot kell legalább venni hogy az integrál értéke 1%-os relatív pontossággal megközelítse az integrál valódi értékét ? Legyen tehát \[I_0=\int_0^1\mathrm{d}x \left (x^2+3x+2\right )=\frac{23}{6}= 3.8333\dots\] és jelölje \(I_n\) az integrál közelítő értékét \(n\) darab mintavételezési pont esetén. Kérdés tehát \(n\) értékéne meghatározása úgy hogy \[\left|\frac{I_0-I_n}{I_0}\right|<0.01\]
Először definiáljuk a vizsgálandó függvényt és ábrázoljuk is a kérdéses \([0,1]\) intervallumon!
#A vizsgálandó függvény
def f(x):
return x**2+3*x+2
#A vizsgálandó függvény az integrálási tartományon ábrázo
xa=linspace(0,1,1000);ya=f(xa);
plot(xa,ya);
ylim(0,6)
xlabel("x",fontsize=16);
ylabel("f(x)",fontsize=16);
grid(True)
Most pedig számoljuk ki a függvény integrálját különböző számú mintavételezési pont esetén. Ábrázoljuk a kapott integrál értékének relatív hibáját a mintavételezési pontok száménak függvényében!
I_0=23./6. #Az integrál valódi értéke. Vajon hogy jön ez ki ?
I_n=[]; #Az In tömb inicializálása, ebbe fogjuk gyűjteni az integrál közelítéseit adott n-re.
relerror=[]#A relerror tömb inicializálása ebbe fogjuk gyűjteni a relatív hibát.
nrange=range(2,10)
#Az adatgyűjtés itt kezdődik
for n in nrange:
x=linspace(0,1,n);#Az [0,1] intervallum egyenletes mintavételezésse n darab helyen
y=f(x); #A függvényértékek
I_n.append(trapez(x,y));# A trapéz szabály eredményeit gyűjtjük az In tömbbe
relerror.append(abs((I_0-trapez(x,y))/I_0)) #ide pedig a relatív hibát
#A relatív hiba ábrázolása
plot(nrange,relerror,'o-');
grid(True);
xlabel("n",fontsize=16);
ylabel("relatív hiba",fontsize=16);
yscale('log')
Ahogy a fenti ábra is jól mutatja a relatív hiba 4 mintavételezési pont esetén már a meghatározott küszöbszint alá esik.
Erősen oszcilláló függvény integrálása és az abszolút hiba¶
Az előző példa egy viszonylag egyszerű függvény integrálása volt, általában numerikus problémák léphetnek fel olyan esetekben ha az integrandus gyorsan oszcillál, vagy ha valamilyen szingularitás van az integrálási tartományon. Vizsgáljunk meg egy kicsit bonyolultabb esetet! Integráljuk a \[g(x)=(x^2+3x+2)\cos(500x)\] függvényt a \([0,2]\) intervallumon, és vizsgáljuk meg a relatív és az abszolút hiba \(|I_0-I_n|\) alakulását a mintavételezési pontok számának függvényében!
# Második próbafüggvény, vegyük észre hogy g(x)=f(x)*cos(500*x) ezt később még fogjuk haszálni!
def g(x):
return (x**2+3*x+2)*numpy.cos(500*x) #itt numpy.cos()-t használunk simán cos() helyett
#erre azért van szükség mert a trapez()-on belülről
#fogjuk meghívni a g() függvényt
Vizsgáljuk meg ezt a függvényt különböző számú mintavételezési ponttal!
# A vizsgálandó függvény alakja különböző számú mintavételezési pontok esetén.
xa=linspace(0,2,1000);ya=g(xa);
plot(xa,ya,label='pontok száma:1000');
xb=linspace(0,2,500);yb=g(xb);
plot(xb,yb,label='pontok száma:500');
xc=linspace(0,2,100);yc=g(xc);
plot(xc,yc,label='pontok száma:100');
legend(loc='upper right',fontsize=10);
xlabel("x",fontsize=16);
ylabel("g(x)",fontsize=16);
grid(True)
Ahogy a fenti ábra is jól illusztrálja, és ahogy a függvény alakjából is sejthettük, egy igen gyorsan oszcilláló függvénnyel van dolgunk! Az első példához hasonlóan határozzuk meg a hibát:
I_02=-3./250000. + 7.*cos(1000.)/250000. + 1499999.*sin(1000.)/62500000. #Az integrál valódi értéke.
#Vajon miért ennyi ?
I_n2=[]; #Az In tömb inicializálása, ebbe fogjuk gyűjteni az integrál közelítéseit adott n-re.
abserror=[]#A abserror tömb inicializálása ebbe fogjuk gyűjteni a abszolút hibát.
relerror=[]#A relerror tömb inicializálása ebbe fogjuk gyűjteni a relatív hibát.
nrange=range(2,2000,30)
#Az adatgyűjtés itt kezdődik
for n in nrange:
x=linspace(0,2,n);#Az [0,2] intervallum egyenletes mintavételezésse n darab helyen
y=g(x); #A függvényértékek
I_n2.append(trapez(x,y));# A trapéz szabály eredményeit gyűjtjük az In tömbbe
abserror.append(abs((I_02-trapez(x,y)))) #ide pedig az abs hibát
relerror.append(abs((I_02-trapez(x,y)))/abs(I_02)) #ide pedig a rel hibát
#A hibák ábrázolása
plot(nrange,abserror,'o-',label='abszolút hiba');
plot(nrange,relerror,'o-',label='relatív hiba');
legend(loc='upper right',fontsize=10);
grid(True);
xlabel("n",fontsize=16);
ylabel("hiba",fontsize=16);
yscale('log')
Jól látszik hogy az integrál pontos meghatározásához jóval több pontra van szükségünk mint az első esetben! Az abszolút hiba 500 mintavételezési pontnál éri el azt a kritikus értéket amit az előző feladatban kiszabtunk, a relatív hiba még 2000 mintavételezési pont esetén sem éri el ezt!
02-Scipy rutin numerikus integrálásra¶
Az előző fejezetben a trapéz formula alkalmazását láttuk két egyszerű esetben. Láttuk azt is hogy bizony előfordulhat hogy az egyszerű trapéz szabály nem feltétlenül a leghatékonyabb módszer a numerikus integrál elvégzésére. Szerencsére rendelkezésre állnak szofisztikáltabb numerikus integráló algoritmusok python csomagok formájában. Egy ilyennel fogunk a továbbiakban megismerkedni. A scipy csomag integrate könyvtárának quad nevű parancsa segítségével egy dimenziós függvények határozott integrálját tudjuk kiszámítani.
from scipy.integrate import quad #a quad parancs betöltése
Egyszerű függvények integrálása a quad() parancs-al¶
Határozzuk meg ismét az \(f(x)\) függvény integrálját a \([0,1]\) intervallumon. Használjuk most a quad() parancsot!
quad(f,0,1) #a syntaxis: quad(f,a,b)
# f: egy egyváltozós függvény
# a: az alsó határ
# b: a felső határ
Figyeljük meg hogy a rutin nem két listát vár a bemeneten, hanem magát az integrandus függvényt! Figyeljük meg hogy a rutin egy szám párost ad eredményül! Ezt komplex számként kell értelmezni! A páros első eleme a valós a második eleme pedig a képzetes rész. Mint látjuk az első elem megegyezik az előző fjezetben kapott értékkel a második pedig gyakorlatilag nulla!
Előfordulhat olyan eset amikor az integrál határai végtelenek ekkor a numpy.inf vagy egyszerűen csak inf határok megadásával jelezzük a rutinnak hogy végtelenig szeretnénk integrálni. Határozzuk meg például a Gauss-görbe alatti területet numerikusan! Az elvégzendő integrál ismert: \[\int_{-\infty}^\infty \mathrm{e}^{-x^2}\mathrm{d}x=\sqrt{\pi} \]
#A Gauss görbe függvény definíciója
def gauss(x):
return exp(-x**2);
#A függvény alakja
x=linspace(-5,5,1000);
plot(x,gauss(x),'r-')
xlabel("x",fontsize=16);
ylabel(r"$\mathrm{e}^{-x^2}$",fontsize=16);
grid(True)
Az integrál meghatározása a quad parancs segítségével, illetve a végeredmény és az analitikus eredmény összehasonlítása:
res=quad(gauss, -inf , inf ) # integrálás végtelen határok között
print res[0] # a numerikus eredmény
print sqrt(pi) # az analitikus eredmény
Numerikusan problémás függvények kezelése a quad() rutinnal¶
Vizsgáljuk meg a \(g(x)\) függvény integrálját is!
res=quad(g,0,2)
print res[0] # a numerikus eredmény
print I02 # az analitikus eredmény
Amint látszik egy elég rossz eredményt kaptunk! Sőt, első futás esetén még egy rózsaszín figyelmeztető blokk is megjelenik. Segíthetünk ezen a problémán ha a quad fügvényt felkészítjük az oscilláló tényezőre a integrandusban! Ezt a következő módon tesszük. A \(g(x)\) függvény helyett az \(f(x)\) et adjuk be a quad függvénynek és egy súlyozott integrál számítását kérjük \(\cos(a x)\) súlyfüggvény jelenlétében azaz \[\int_0^2g(x)\mathrm{d}x=\int_0^2f(x)w(x)\mathrm{d}x=\int_0^2f(x)\cos(a x)\mathrm{d}x.\] Az \(a\) változó értékét pedig a \(\cos()\) függvényben szereplő \(500\)-as értékre állítjuk.
res=quad(f, #g helyett f
0, #a határok változatlanok
2,
weight='cos', #a súlyfüggvény
wvar=500.) #a súlyfügvény paramétere
print res[0] # a numerikus eredmény
print I02 # az analitikus eredmény
Így a számított eredmény már nagy pontossággal megegyezik az analitikus értékkel!
Előfordulhat hogy az integrandus a számunkra érdekes intervallum belsejében valahol szingularitást mutat, azaz értéke végtelenné válik, vegyük például a \[h(x)=\sqrt[3]{\frac{1}{(x-1)^2}}\] függvényt mely a \(x=1\) esetén divergál:
#A függvény definíciója, figyeljük meg hogy a -2 -es illetve az 1/3-as hatványkitevőket külön kezeljük!Vajon miért ?
def h(x):
return ((x-1.0)**(-2))**(1.0/3.0)
#A h(x) függvény ábrázolása
x=linspace(0,2,1000);
plot(x,h(x));
xlabel("x",fontsize=16);
ylabel("h(x)",fontsize=16);
A quad függvény egyszerű hívására végtelen eredményt, esetleg valamilyen hiba üzenetet kapunk, hiszen ha a mintavételezés során éppen eltaláljuk a szingularitást akkor az integrált közelítő sorozat egy végtelen értékű elemmel lesz gazdagabb.
quad(h,0.0,2.0) #Ez így nem fog menni!
Ha a szingularitások helye ismert akkor a points paraméter segítségével a quad rutin tudomására hozhatjuk hogy ezekben a pontokban valami problémára számíthat a függvény kiértékelse során.
res=quad(h,0.0,2.0,points=[1.0]) #Így már igen!
print res[0] # a numerikus eredmény
print 6 # az analitikus eredmény, vajon hogy jött ez ki ?
03-Szmbolikus integrálás sympy rutinok segítségével¶
A fenti eredmények kiértékelésére néhány helyen felhasználtunk analitikus eredményeket is. A sympy csomag segítségével néhány alapvető analitikus formula manipulálási készség is rendelkezésünkre áll. Az alábbiakban ennek a csomagnak a segítségével a fenti numerikus integrálokat analitikusan is kiértékeljük.
import sympy #a sympy szimbolikus csomag betöltése
sympy.init_printing() #a szimbolikus kifejezések "szép" megjelenítése
Ahhoz hogy a sympy függvények egy objektumot analitikus változóként kezeljenek először meg kell őket jelölni mint analitikus szimbólumok:
x1, y1, z1, p1 = sympy.symbols('x1 y1 z1 p1') # az x1 y1 és z1 változók felkészítése symbolikus számításokhoz
Figyelem! A már megjelölt változók a notebook további részében már nem használhatók szokásos változóként!
A sympy parancsai közül az integrate() parancs határozott és határozatlan integrálok elvégzésére szolgál. Vegyük például az alábbi ismert integrálokat:
$ $
\(\displaystyle{\int_{0}^{\pi/2} \sin(x)\mathrm{d}x=? }\)
\(\displaystyle{\int_{-\infty}^\infty \mathrm{e}^{-x^2}\mathrm{d}x=? }\)
Határozatlan integrálokat az integrandus és az integrálási változó megadásával tudunk számítani:
sympy.integrate(x1**p1,x1) #Egy határozatlan integrál
Határozott integálok számításához meg kall adnunk az integrálási tartományt:
sympy.integrate(sympy.sin(x1),(x1,0,pi/2)) #Egy határozott integrál
Az integrálási tartomány végpontjai lehetnek végtelenk is!
sympy.integrate(sympy.exp(-x1**2),(x1,-sympy.oo,sympy.oo)) #A végtelent itt "sympy.oo" jelöli és nem inf!!
sympy.integrate(sympy.exp(-x1**2),(x1,-inf,inf)) #De mivel a scipy is be van töltve ezért ez is értelmes...
Végül határozzuk meg az előző két fejezetben vizsgált integrálokat immár analitikusan is!
Az első feladat egyszerű polinomiális integrandusa \(\displaystyle\int_0^1 x^2+3x+2 \mathrm{d}x=\)
result=sympy.integrate(x1**2+3*x1+2,(x1,0,1))
print result
print sympy.N(result) #Az analitikus eredmény numerikus kiértékelése
A második feladat erősen oszcilláló integrandusa \(\displaystyle\int_0^2 \left(x^2+3x+2\right)\cos(500x) \mathrm{d}x=\)
result=(sympy.integrate((x1**2+3*x1+2)*sympy.cos(500*x1),(x1,0,2)))
print result
print sympy.N(result)
A harmadik feladat szinguláris integrandusa \(\displaystyle\int_0^2 \sqrt[3]{(x-1)^{-2}} \mathrm{d}x=\)
result=sympy.integrate(sympy.cbrt(power((x1-1),-2)),(x1,0,2))
print result
print sympy.N(result)